TERCEIRA QUANTIZAÇÃO E RELATIVIDADE SDCITE GRACELI EM:
POSTULADOS DE GRACELI PARA ENTROPIA E TERMODINÂMICA.
1] DENTRO DE UM SISTEMA TANTO A ENTROPIA QUANTO A ENTALPIA VARIAM E NÃO VOLTAM AO SEU ESTADO INICIAL CONFORME O SDCTIE GRACELI.
2] ISTO SERVE PARA TODAS AS LEIS DA TERMODINÂMICA, E OUTROS RAMOS DA FÍSICA, INCLUSIVE PARA FÍSICA QUÂNTICA, CONDUTIVIDADE E ELETROMAGNETISMO.
A TEMPERATURA QUE ALTERA AS VIBRAÇÕES E OS FLUXOS DAS ENERGIAS, DIMENSÕES E FENÔMENOS TAMBÉM ALTERA OS SPINS, MOMENTUNS, MOMENTUNS MAGNÉTICOS, E OUTROS.
CONDE COM ISTO SE TEM NOVOS NÚMEROS QUÂNTICO DE GRACELI [TEMPERATURA, VIBRAÇÕES, E FLUXOS VARIACIONAIS.]
ONDE SE FORMA UMA NOVA FÍSICA QUÂNTICA, DE CONDUTIVIDADE, ELÉTRICA, MAGNÉTICA, ELETROMAGNÉTICA, MODELO PADRÃO, SIMETRIAS, DINÂMICAS, E MECÂNICAS.
COM AÇÃO E VARIAÇÕES SOBRE A QUÍMICA, A FÍSICA, RELATIVIDADES, E OUTROS.
OU SEJA, UM SISTEMA GENERALIZADO VARIACIONAL SOBRE TODAS AS FÍSICAS, QUÍMICAS,E BIOLOGIA MOLECULAR, E SUAS RAMIFICAÇÕES.
sexta-feira, 21 de agosto de 2020
CONFORME AUMENTA A TEMPERATURA, TAMBÉM APROXIMADAMENTE AUMENTA A DILATAÇÃO [CONFORME OS MATERIAIS DENTRO DO SISTEMA SDCTIE GRACELI] COM ISTO AUMENTA AS VIBRAÇÕES, SPINS, NÚMEROS QUÂNTICO DE GRACELI, ESTRUTURA ELETRÕNICA, E ESTADOS QUÂNTICO, COM ISTO SE TEM UM SISTEMA VARIACIONAL EM TODAS AS TEORIAS E PRINCÍPIOS, E FUNDAMENTOS ENVOLVENDO MODELO ATÕMICO, QUÍMICA QUÂNTICA, E TODA A MECÂNICA QUÂNTICA, COMO E ENTRE TANTAS TEORIAS COM A INCERTEZA, EXCLUSÃO, ÁTOMO DE BOHR E OUTROS, EQUAÇÕES DA PRIMEIRA E SEGUNDA TEORIA QUÂNTICA, COOMO TAMBÉM TODA TEORIA ENVOLVENDO A TERCEIRA TEORIA QUANTICA SDCTIE GRACELI.
OU SEJA, SE TEM UMA TEORIA E MECÂNICA QUÂNTICA VARIACIONAL CONFORME SE ENCONTRA EM ÍNDICES E TIPOS DE INTENSIDADES DE TEMPERATURA.
O MESMO ACONTECE PARA A ELETROSTÁTICA, ELETROMAGNETISMO, TEORIA DE PARTÍCULAS, GAUGE, SIMETRIAS, PARIDADES, MODELO PADRÃO TÉRMICO, E OUTROS.
VEJAMOS EM:
TERCEIRA QUANTIZAÇÃO PELO SDCTIE GRACELI
TRANS-QUÂNTICA SDCTIE GRACELI, TRANSCENDENTE, RELATIVISTA SDCTIE GRACELI, E TRANS-INDETERMINADA.
FUNDAMENTA-SE EM QUE TODA FORMA DE REALIDADE SE ENCONTRA EM TRANSFORMAÇÕES, INTERAÇÕES, TRANSIÇÕES DE ESTADOS [ESTADOS DE GRACELI], ENERGIAS E FENÔMENOS DENTRO DE UM SISTEMA DE DEZ OU MAIS DIMENSÕES DE GRACELI, E CATEGORIAS DE GRACELI.
FUNÇÃO GERAL GRACELI DA TRANS- INDETERMINALIDADE PELO SDCTIE GRACELI
FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI. E DE ESTADOS TRANSICIONAIS =
TRANSFORMAÇÕES ⇔ INTERAÇÕES ⇔ TUNELAMENTO ⇔ EMARANHAMENTO ⇔ CONDUTIVIDADE ⇔ DIFRAÇÕES ⇔ estrutura eletrônica, spin, radioatividade, ABSORÇÕES E EMISSÕES INTERNA ⇔ Δ de temperatura e dinâmicas, transições de estados quântico Δ ENERGIAS, ⇔ Δ MASSA , ⇔ Δ CAMADAS ORBITAIS , ⇔ Δ FENÔMENOS , ⇔ Δ DINÂMICAS, ⇔ Δ VALÊNCIAS, ⇔ Δ BANDAS, Δ entropia e de entalpia, E OUTROS.
x [EQUAÇÃO DE DIRAC].
+ FUNÇÃO TÉRMICA.
+ FUNÇÃO DE RADIOATIVIDADE
, + FUNÇÃO DE TUNELAMENTO QUÂNTICO.
+ ENTROPIA REVERSÍVEL
+ FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA
ENERGIA DE PLANCK
X
V [R] [MA] = Δe,M, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM......ΤDCG
XΔe, ΔM, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM...... =
x
sistema de dez dimensões de Graceli + DIMENSÕES EXTRAS DO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.[como, spins, posicionamento, afastamento, ESTRUTURA ELETRÔNICA, e outras já relacionadas]..
- DIMENSÕES DE FASES DE ESTADOS DE TRANSIÇÕES DE GRACELI.
xsistema de transições de estados, e estados de Graceli, fluxos aleatórios quântico, potencial entrópico e de entalpia. [estados de transições de fases de estados de estruturas, quântico, fenomênico, de energias, e dimensional [sistema de estados de Graceli].x
número atômico, estrutura eletrônica, níveis de energia - TEMPO ESPECÍFICO E FENOMÊNICO DE GRACELI.
- X
- CATEGORIAS DE GRACELI
- T l T l E l Fl dfG l
X [ESTADO QUÂNTICO]
A entropia de transferência é uma medida estatística não paramétrica que mede a quantidade de informação direcional que é transferida entre dois processos aleatórios[1][2][3][4]. A entropia de transferência de um processo X para outro Y é definida como a redução da incerteza sobre os valores futuros de Y quando se conhecem os valores passados de X dados valores passados de Y.
Matematicamente, sejam e dois processos aleatórios definidos no tempo . Utilizando a entropia da informação de Shannon, H(X), a entropia de transferência pode ser calculada como:
Alternativamente, a entropia de transferência pode ser descrita em termos da informação mútua condicional[5][6], aonde o termo condicionado é o passado da variável Y, isto é, :
A entropia de transferência torna-se o teste de causalidade de Granger quando o processo é autoregressivo e satisfaz as condições para causalidade de Granger sempre.[7] Desta forma, torna-se mais adequado utilizar a entropia de transferência para o teste de causalidade de Granger quando o sinal é não-linear. [8][9]O ponto negativo deta abordagem é a necessidade de maior número de amostras para uma estimativa confiável do valor obtido.[10]
Embora tenha sido definido para análise bivariada, existem extensões da entropia de transferência para análise multivariada, seja criando condicionais às demais variáveis[11] ou considerando a transferência de informação de um conjunto de fontes[12]. Porém, ambas as alternativas exigem mais dados.
A entropia de transferência tem sido aplicada para a investigação de conectividade funcional no cérebro e em sistemas de neurônios[13][14][15], medir a influência de indivíduos/grupos em redes sociais[8] e como método de identificação de precursores de terremotos[16]
Em teoria das probabilidades e Teoria da Informação, a informação mútua (em inglês MI de en:Mutual information) de duas variáveis aleatórias é a medida da dependência mútua entre as duas variáveis. Mais especificamente, a informação mútua quantifica a informação (em unidades como shannons, mais conhecidos como bits) que uma variável aleatória contém acerca da outra. O conceito de informação mútua esta intrinsicamente ligado ao da Entropia de uma variável aleatória, uma noção fundamental da teoria da informação, que define a "quantidade de informação" contida em uma variável aleatória.
Não sendo limitado a variáveis aleatória com valores reais como o coeficiente de correlação, a MI é mais genérica e determina quão similar a distribuição conjunta p(X,Y) está dos produtos das distribuições marginais p(X)p(Y). MI é o valor esperado da pointwise mutual information (PMI).
TRANSFORMAÇÕES ⇔ INTERAÇÕES ⇔ TUNELAMENTO ⇔ EMARANHAMENTO ⇔ CONDUTIVIDADE ⇔ DIFRAÇÕES ⇔ estrutura eletrônica, spin, radioatividade, ABSORÇÕES E EMISSÕES INTERNA ⇔ Δ de temperatura e dinâmicas, transições de estados quântico Δ ENERGIAS, ⇔ Δ MASSA , ⇔ Δ CAMADAS ORBITAIS , ⇔ Δ FENÔMENOS , ⇔ Δ DINÂMICAS, ⇔ Δ VALÊNCIAS, ⇔ Δ BANDAS, Δ entropia e de entalpia, E OUTROS.
+ FUNÇÃO TÉRMICA.
+ FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA
V [R] [MA] = Δe,M, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM......ΤDCG XΔe, ΔM, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM...... =
xsistema de dez dimensões de Graceli +DIMENSÕES EXTRAS DO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.[como, spins, posicionamento, afastamento, ESTRUTURA ELETRÔNICA, e outras já relacionadas]..- DIMENSÕES DE FASES DE ESTADOS DE TRANSIÇÕES DE GRACELI.xsistema de transições de estados, e estados de Graceli, fluxos aleatórios quântico, potencial entrópico e de entalpia. [estados de transições de fases de estados de estruturas, quântico, fenomênico, de energias, e dimensional [sistema de estados de Graceli].x
- TEMPO ESPECÍFICO E FENOMÊNICO DE GRACELI.
- X
- CATEGORIAS DE GRACELI
- DT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLl
A entropia de transferência é uma medida estatística não paramétrica que mede a quantidade de informação direcional que é transferida entre dois processos aleatórios[1][2][3][4]. A entropia de transferência de um processo X para outro Y é definida como a redução da incerteza sobre os valores futuros de Y quando se conhecem os valores passados de X dados valores passados de Y.
Matematicamente, sejam e dois processos aleatórios definidos no tempo . Utilizando a entropia da informação de Shannon, H(X), a entropia de transferência pode ser calculada como:
Alternativamente, a entropia de transferência pode ser descrita em termos da informação mútua condicional[5][6], aonde o termo condicionado é o passado da variável Y, isto é, :
A entropia de transferência torna-se o teste de causalidade de Granger quando o processo é autoregressivo e satisfaz as condições para causalidade de Granger sempre.[7] Desta forma, torna-se mais adequado utilizar a entropia de transferência para o teste de causalidade de Granger quando o sinal é não-linear. [8][9]O ponto negativo deta abordagem é a necessidade de maior número de amostras para uma estimativa confiável do valor obtido.[10]
Embora tenha sido definido para análise bivariada, existem extensões da entropia de transferência para análise multivariada, seja criando condicionais às demais variáveis[11] ou considerando a transferência de informação de um conjunto de fontes[12]. Porém, ambas as alternativas exigem mais dados.
A entropia de transferência tem sido aplicada para a investigação de conectividade funcional no cérebro e em sistemas de neurônios[13][14][15], medir a influência de indivíduos/grupos em redes sociais[8] e como método de identificação de precursores de terremotos[16]
Em teoria das probabilidades e Teoria da Informação, a informação mútua (em inglês MI de en:Mutual information) de duas variáveis aleatórias é a medida da dependência mútua entre as duas variáveis. Mais especificamente, a informação mútua quantifica a informação (em unidades como shannons, mais conhecidos como bits) que uma variável aleatória contém acerca da outra. O conceito de informação mútua esta intrinsicamente ligado ao da Entropia de uma variável aleatória, uma noção fundamental da teoria da informação, que define a "quantidade de informação" contida em uma variável aleatória.
Não sendo limitado a variáveis aleatória com valores reais como o coeficiente de correlação, a MI é mais genérica e determina quão similar a distribuição conjunta p(X,Y) está dos produtos das distribuições marginais p(X)p(Y). MI é o valor esperado da pointwise mutual information (PMI).
Índice
Definição
Formalmente a informação mútua[1] de duas variáveis aleatórias discretas, X e Y pode ser definida como:
aonde p(x,y) é a distribuição de probabilidade conjunta de X e Y, e e são funções de probabilidade de distribuição marginal de X e Y, respectivamente. No caso de variáveis aleatórias contínuas, a somatória é substituída por uma integral dupla definida:
aonde p(x,y) é agora a função de densidade de probabilidade conjunta de X e Y, p(x) e p(y) são funções de densidade de probabilidade marginal de X e Y, respectivamente.
Se usarmos o logarítmo de base 2 a unidade da informação mútua será bits.
Formalmente a informação mútua[1] de duas variáveis aleatórias discretas, X e Y pode ser definida como:
aonde p(x,y) é a distribuição de probabilidade conjunta de X e Y, e e são funções de probabilidade de distribuição marginal de X e Y, respectivamente. No caso de variáveis aleatórias contínuas, a somatória é substituída por uma integral dupla definida:
aonde p(x,y) é agora a função de densidade de probabilidade conjunta de X e Y, p(x) e p(y) são funções de densidade de probabilidade marginal de X e Y, respectivamente.
Se usarmos o logarítmo de base 2 a unidade da informação mútua será bits.
Motivação
Intuitivamente, a informação mútua mede a informação compartilhada entre X e Y: ela mede quanto o conhecimento de uma destas variáveis reduz a incerteza sobre a outra. Por exemplo, se X e Y são independentes, então conhecer X não fornece nenhuma informação sobre Y e vice versa, então a informação mútua delas será zero. No outro extremo, se X for uma função determinística de Y e Y for uma função determinística de X então toda a informação contida em X é compartilhada por Y: conhecer X determina o valor de Y e vice versa. Como resultado, neste caso a informação mútua é o mesmo que a incerteza contida em Y (ou X) sozinha, chamada de entropia de Y (ou X). Além disto, esta informação mútua é a mesma que a entropia de X e também que a entropia de Y. (Um caso bem especial disto é quando X e Y são a mesma variável aleatória.)
Informação mútua é uma medida da dependência inerente expressada pela distribuição de probabilidade conjunta de X e Y relativas à distribuição conjuntas de X e Y assumindo que sejam independentes. Informação mútua portanto mede a dependência no sentido que: I(X; Y) = 0 se e somente se X e Y são variáveis aleatórias independentes. Isto é fácil de ver num dos sentidos: se X e Y são independentes, então p(x,y) = p(x)p(y), e portanto:
Além disto, a informação mútua é não-negativa (i.e. I(X;Y) ≥ 0; veja abaixo) e uma função simétrica (i.e. I(X;Y) = I(Y;X)).
Intuitivamente, a informação mútua mede a informação compartilhada entre X e Y: ela mede quanto o conhecimento de uma destas variáveis reduz a incerteza sobre a outra. Por exemplo, se X e Y são independentes, então conhecer X não fornece nenhuma informação sobre Y e vice versa, então a informação mútua delas será zero. No outro extremo, se X for uma função determinística de Y e Y for uma função determinística de X então toda a informação contida em X é compartilhada por Y: conhecer X determina o valor de Y e vice versa. Como resultado, neste caso a informação mútua é o mesmo que a incerteza contida em Y (ou X) sozinha, chamada de entropia de Y (ou X). Além disto, esta informação mútua é a mesma que a entropia de X e também que a entropia de Y. (Um caso bem especial disto é quando X e Y são a mesma variável aleatória.)
Informação mútua é uma medida da dependência inerente expressada pela distribuição de probabilidade conjunta de X e Y relativas à distribuição conjuntas de X e Y assumindo que sejam independentes. Informação mútua portanto mede a dependência no sentido que: I(X; Y) = 0 se e somente se X e Y são variáveis aleatórias independentes. Isto é fácil de ver num dos sentidos: se X e Y são independentes, então p(x,y) = p(x)p(y), e portanto:
Além disto, a informação mútua é não-negativa (i.e. I(X;Y) ≥ 0; veja abaixo) e uma função simétrica (i.e. I(X;Y) = I(Y;X)).
Propriedades
• ;
• se, e somente se, X e Y forem variáveis aleatórias independentes;
•
Dada a forte relação entre Informação Mútua e Entropia, temos os seguintes corolários:
• , ;
•
• ;
• se, e somente se, X e Y forem variáveis aleatórias independentes;
•
Dada a forte relação entre Informação Mútua e Entropia, temos os seguintes corolários:
• , ;
•
Relação com outras quantidades
Não-negatividade
Usando a Desigualdade de Jensen na definição da informação mútua podemos mostrar que I(X;Y) é não-negativa, i.e.
Usando a Desigualdade de Jensen na definição da informação mútua podemos mostrar que I(X;Y) é não-negativa, i.e.
Relação com a entropia condicional e conjunta
Informação mútua pode ser expressada equivalentemente como
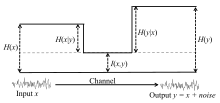
aonde e são entropias marginais, Η(X|Y) e Η(Y|X) são as entropias condicionais, e Η(X,Y) é a entropia conjunta de X e Y. Note a analogia da união, diferença e intersecção de dois conjuntos, conforme ilustrado no diagrama de Venn. Em termos de canais de comunicação nos quais a saída é uma versão ruídosa da entrada , essas relações estão resumidas na figura abaixo.
Como I(X;Y) é não-negativa, consequentemente, . Aqui temos a dedução detalhada de I(X;Y) = Η(Y) – Η(Y|X):
As provas das outras identidades acima são similares.
Intuitivamente, se a entropia H(Y) é considerada como uma medida da incerteza sobre uma variável aleatória, então H(Y|X) é uma medida do quanto X não diz sobre Y. Isto é "a quantidade de incerteza restando sobre Y depois que X é conhecido", e então o lado direito da primeira dessas igualdades pode ser lido como "a quantidade de incerteza em Y, menos a quantidade de incerteza em Y que sobra após X ser conhecido", que é equivalente à "quantidade de incerteza em Y que é removida por conhecer X". O que corrobora o sentido intuitivo da informação mútua como a quantidade de informação (ou seja, redução da incerteza) que conhecer qualquer variável produz sobre a outra.
Note que no caso discreto H(X|X) = 0 e portanto Η(X) = I(X;X). Então Thus I(X;X) ≥ I(X;Y), e pode-se formular o princípio básico que uma variável contém pelo menos tanta informação sobre sí mesma quanto qualquer outra variável pode fornecer.
Entropia, quando relacionada à termodinâmica, é a medida do grau de irreversibilidade de um determinado sistema. Então, quanto menor a chance do sistema voltar ao seu estado original, maior será o grau de entropia. É considerada por Einstein como a primeira lei de todas a ciências.
Para a área de Teoria da Informação, a entropia é definida como sendo uma forma de medir o grau médio de incerteza a respeito de fontes de informação, o que consequentemente permite a quantificação da informação presente que flui no sistema. Em termos simples, o conceito de entropia se associa à ideia de que, quanto mais incerto é o resultado de um experimento aleatório, maior é a informação que se obtém ao observar a sua ocorrência.
Informação mútua pode ser expressada equivalentemente como
aonde e são entropias marginais, Η(X|Y) e Η(Y|X) são as entropias condicionais, e Η(X,Y) é a entropia conjunta de X e Y. Note a analogia da união, diferença e intersecção de dois conjuntos, conforme ilustrado no diagrama de Venn. Em termos de canais de comunicação nos quais a saída é uma versão ruídosa da entrada , essas relações estão resumidas na figura abaixo.
Como I(X;Y) é não-negativa, consequentemente, . Aqui temos a dedução detalhada de I(X;Y) = Η(Y) – Η(Y|X):
As provas das outras identidades acima são similares.
Intuitivamente, se a entropia H(Y) é considerada como uma medida da incerteza sobre uma variável aleatória, então H(Y|X) é uma medida do quanto X não diz sobre Y. Isto é "a quantidade de incerteza restando sobre Y depois que X é conhecido", e então o lado direito da primeira dessas igualdades pode ser lido como "a quantidade de incerteza em Y, menos a quantidade de incerteza em Y que sobra após X ser conhecido", que é equivalente à "quantidade de incerteza em Y que é removida por conhecer X". O que corrobora o sentido intuitivo da informação mútua como a quantidade de informação (ou seja, redução da incerteza) que conhecer qualquer variável produz sobre a outra.
Note que no caso discreto H(X|X) = 0 e portanto Η(X) = I(X;X). Então Thus I(X;X) ≥ I(X;Y), e pode-se formular o princípio básico que uma variável contém pelo menos tanta informação sobre sí mesma quanto qualquer outra variável pode fornecer.
Entropia, quando relacionada à termodinâmica, é a medida do grau de irreversibilidade de um determinado sistema. Então, quanto menor a chance do sistema voltar ao seu estado original, maior será o grau de entropia. É considerada por Einstein como a primeira lei de todas a ciências.
Para a área de Teoria da Informação, a entropia é definida como sendo uma forma de medir o grau médio de incerteza a respeito de fontes de informação, o que consequentemente permite a quantificação da informação presente que flui no sistema. Em termos simples, o conceito de entropia se associa à ideia de que, quanto mais incerto é o resultado de um experimento aleatório, maior é a informação que se obtém ao observar a sua ocorrência.
Índice
Contexto Histórico
O engenheiro e matemático Claude Shannon é considerado o pai da teoria da informação. Americano, atuou nas áreas de engenharia elétrica, comunicações, criptografia e xadrez computacional, instalando bases tanto para a indústria de computadores quanto para a de telecomunicações. Shannon introduziu, em 1948, no trabalho A Mathematical Theory of Communication,[1] publicado na revista Bell System Technical Journal, conceitos primordiais que deram origem à teoria da informação, entre eles a entropia da informação e a capacidade de canal.
Nesse trabalho, Shannon desenvolve um modelo teórico para o problema da comunicação envolvendo a transmissão de mensagens digitais. Ele parte do pressuposto de que uma mensagem transmitida para um receptor é invariavelmente recebida com ruídos, isto é, quando uma informação passa por um canal de comunicação ela sofre distorções e chega ao receptor precisando ser submetida a um processo de decodificação.
Shannon então demonstrou matematicamente que, se por exemplo consideramos a transmissão de um sinal ruidoso como uma conversa barulhenta, este pode ser recuperado no transmissor sem distorção, respeitadas características como a capacidade de transmissão daquele meio (canal). Basta nesse sentido empregar um código corretor de erros adequado, de modo que os sinais serão recebidos com probabilidade de erro arbitrariamente pequena.
Norbert Wiener, na mesma época, associou entropia ao processo de comunicação ou informação, afirmando que, nos processos onde há perda de informação, há uma situação igual aos processos que ganham entropia. Segundo Wiener, a soma de informação em um sistema é a medida de seu grau de organização e, ao mesmo tempo, de seu grau de desorganização, sendo assim, um é o negativo do outro.
As definições de Shannon tiveram impacto direto no desenvolvimento das comunicações, da criptografia, da computação digital, da codificação de sinais (vídeo, imagem, texto), assim como em problemas da linguística, psicologia e fonética. A linguagem, por exemplo, é um mecanismo de comunicação que tem um código de correção de erros embutido nas suas regras de sintaxe, ortografia e semântica.
O engenheiro e matemático Claude Shannon é considerado o pai da teoria da informação. Americano, atuou nas áreas de engenharia elétrica, comunicações, criptografia e xadrez computacional, instalando bases tanto para a indústria de computadores quanto para a de telecomunicações. Shannon introduziu, em 1948, no trabalho A Mathematical Theory of Communication,[1] publicado na revista Bell System Technical Journal, conceitos primordiais que deram origem à teoria da informação, entre eles a entropia da informação e a capacidade de canal.
Nesse trabalho, Shannon desenvolve um modelo teórico para o problema da comunicação envolvendo a transmissão de mensagens digitais. Ele parte do pressuposto de que uma mensagem transmitida para um receptor é invariavelmente recebida com ruídos, isto é, quando uma informação passa por um canal de comunicação ela sofre distorções e chega ao receptor precisando ser submetida a um processo de decodificação.
Shannon então demonstrou matematicamente que, se por exemplo consideramos a transmissão de um sinal ruidoso como uma conversa barulhenta, este pode ser recuperado no transmissor sem distorção, respeitadas características como a capacidade de transmissão daquele meio (canal). Basta nesse sentido empregar um código corretor de erros adequado, de modo que os sinais serão recebidos com probabilidade de erro arbitrariamente pequena.
Norbert Wiener, na mesma época, associou entropia ao processo de comunicação ou informação, afirmando que, nos processos onde há perda de informação, há uma situação igual aos processos que ganham entropia. Segundo Wiener, a soma de informação em um sistema é a medida de seu grau de organização e, ao mesmo tempo, de seu grau de desorganização, sendo assim, um é o negativo do outro.
As definições de Shannon tiveram impacto direto no desenvolvimento das comunicações, da criptografia, da computação digital, da codificação de sinais (vídeo, imagem, texto), assim como em problemas da linguística, psicologia e fonética. A linguagem, por exemplo, é um mecanismo de comunicação que tem um código de correção de erros embutido nas suas regras de sintaxe, ortografia e semântica.
Aplicações diversas da Entropia
Nos anos seguintes a criação do conceito, outros pesquisadores o modificaram e generalizaram, criando outras formas de entropia. Logo, o conceito da entropia de informação foi aplicado nas mais diversas áreas de conhecimento, como por exemplo Ciência da Informação, biologia, medicina, ecologia, economia e linguística, assim se tornando cada vez mais um método interdisciplinar.
Um dos exemplos da consequência de entropia é o primeiro experimento relacionado à química que demonstra uma auto-organização de partículas duras, não-biológicas, sem ajuda de interações atrativas, como ligações químicas. Cristais complexos foram criados sem a ajuda de interações, como por exemplo os tetraedros se organizaram espontaneamente em um quasicristal, este, por vez, terá suas propriedades diferentes de um cristal ou de um sólido comum, ele poderá ter propriedade ópticas únicas.
Na termodinâmica, a entropia tem um papel fundamental, pois é com não-conservação da entropia, ou seja, com a variação de desordem do sistema que máquinas térmicas funcionam. A compreensão do funcionamento dessas máquinas leva ao conceito da entropia do sistema.
Nos anos seguintes a criação do conceito, outros pesquisadores o modificaram e generalizaram, criando outras formas de entropia. Logo, o conceito da entropia de informação foi aplicado nas mais diversas áreas de conhecimento, como por exemplo Ciência da Informação, biologia, medicina, ecologia, economia e linguística, assim se tornando cada vez mais um método interdisciplinar.
Um dos exemplos da consequência de entropia é o primeiro experimento relacionado à química que demonstra uma auto-organização de partículas duras, não-biológicas, sem ajuda de interações atrativas, como ligações químicas. Cristais complexos foram criados sem a ajuda de interações, como por exemplo os tetraedros se organizaram espontaneamente em um quasicristal, este, por vez, terá suas propriedades diferentes de um cristal ou de um sólido comum, ele poderá ter propriedade ópticas únicas.
Na termodinâmica, a entropia tem um papel fundamental, pois é com não-conservação da entropia, ou seja, com a variação de desordem do sistema que máquinas térmicas funcionam. A compreensão do funcionamento dessas máquinas leva ao conceito da entropia do sistema.
Entropia e Informação
Informação, de acordo com diferentes autores, é um termo que vem sendo usado mais a partir da década de 1950. É usado para significar mensagens, notícias, novidades, dados, conhecimento, literatura, símbolos, signos e, até mesmo, "dicas" e sugestões. Pode até parecer um termo vago, sendo necessário um contexto em que é empregada. Georges Ifrah apresenta pelo menos 26 diferentes conceitos de informação
Diferentemente da energia, a informação é algo que se cria e que existe cada vez mais em maior quantidade no nosso Universo. Segundo Zdenek Zeman, "a expressão da informação de um sistema tem por base, como se sabe, a fórmula matemática da entropia negativa". Partido dessa ideia, informação, isto é, de entropia negativa, pode exprimir, também, a medida da ordem de um sistema nervoso ou de um sistema social. A entropia negativa é atingida quando a probabilidade de ocorrer todos os símbolos é igual, ou seja, é equiprovável e não há a tendência de ocorrer determinado grupo de símbolos.
Shannon abordou, também o conceito de redundância é relacionado à entropia no sentido de que a redundância é tudo o que não é fundamental para ser entendido em uma determinada mensagem, ou seja, é entendida como algo complementar. Então é a medida de entropia para que a mensagem atinja a entropia máxima.
No trabalho desenvolvido por ele em A Teoria Matemática da Comunicação onde é abordada a relação entre a entropia e a informação, Shannon faz a afirmação que a informação contida em uma mensagem pode ser medida pela quantidade de entropia que, por sua vez, é relacionada à frequência dos grupo de símbolos que são transmitidos.
A teoria da informação afirma que quanto menos informações sobre um sistema, maior será sua entropia. A quantidade de informação de uma mensagem é entendida na teoria da informação como sendo o menor número de bits, unidade de informação, necessários para conter todos os valores ou significados desta mensagem. Por exemplo, se quisermos transmitir ou armazenar os números dos meses do ano, serão necessários, no mínimo, 4 bits para representar esta informação. Portanto, a quantidade de informação de uma mensagem é medida pela entropia da mensagem, a qual mede, também a sua incerteza, que é expressa pelo número de bits que precisam ser recuperados quando a mensagem está cifrada para obter novamente um texto claro.
Informação, de acordo com diferentes autores, é um termo que vem sendo usado mais a partir da década de 1950. É usado para significar mensagens, notícias, novidades, dados, conhecimento, literatura, símbolos, signos e, até mesmo, "dicas" e sugestões. Pode até parecer um termo vago, sendo necessário um contexto em que é empregada. Georges Ifrah apresenta pelo menos 26 diferentes conceitos de informação
Diferentemente da energia, a informação é algo que se cria e que existe cada vez mais em maior quantidade no nosso Universo. Segundo Zdenek Zeman, "a expressão da informação de um sistema tem por base, como se sabe, a fórmula matemática da entropia negativa". Partido dessa ideia, informação, isto é, de entropia negativa, pode exprimir, também, a medida da ordem de um sistema nervoso ou de um sistema social. A entropia negativa é atingida quando a probabilidade de ocorrer todos os símbolos é igual, ou seja, é equiprovável e não há a tendência de ocorrer determinado grupo de símbolos.
Shannon abordou, também o conceito de redundância é relacionado à entropia no sentido de que a redundância é tudo o que não é fundamental para ser entendido em uma determinada mensagem, ou seja, é entendida como algo complementar. Então é a medida de entropia para que a mensagem atinja a entropia máxima.
No trabalho desenvolvido por ele em A Teoria Matemática da Comunicação onde é abordada a relação entre a entropia e a informação, Shannon faz a afirmação que a informação contida em uma mensagem pode ser medida pela quantidade de entropia que, por sua vez, é relacionada à frequência dos grupo de símbolos que são transmitidos.
A teoria da informação afirma que quanto menos informações sobre um sistema, maior será sua entropia. A quantidade de informação de uma mensagem é entendida na teoria da informação como sendo o menor número de bits, unidade de informação, necessários para conter todos os valores ou significados desta mensagem. Por exemplo, se quisermos transmitir ou armazenar os números dos meses do ano, serão necessários, no mínimo, 4 bits para representar esta informação. Portanto, a quantidade de informação de uma mensagem é medida pela entropia da mensagem, a qual mede, também a sua incerteza, que é expressa pelo número de bits que precisam ser recuperados quando a mensagem está cifrada para obter novamente um texto claro.
Entropia como conceito da Teoria da Informação
A Teoria da Informação teve inicialmente como destaque as questões técnicas, sendo uma das primeiras teorias a separar com nitidez a informação da significação. A Teoria da Informação está situada dentro da cibernética, onde a informação se mostra como uma medida probabilística. Esta teoria tem um grande interesse pelo funcionamento dos sinais, pelas transformações energéticas mediante a codificação da mensagem e sua de codificação. Ela opera com os seguintes conceitos:
- ruído;
- redundância;
- entropia;
- imprevisibilidade.
Em fontes contínuas, a codificação da informação gera ruído na mensagem, isso se dá pelo fato de que a fonte contínua precisaria de um vasto repertório de símbolos e que, como consequência, necessitaria uma capacidade de transmissão grande e, como é sabido, não existe um canal livre de ruído.
Shannon abordou, também o conceito de redundância é relacionado à entropia no sentido de que a redundância é tudo o que não é fundamental para ser entendido em uma determinada mensagem, ou seja, é entendida como algo complementar. Então é a medida de entropia para que a mensagem atinja a entropia máxima.
A entropia desejada de uma informação é a máxima que é dada pelas probabilidades equivalentes de ocorrer todos os símbolos.
A teoria da informação não estuda uma língua pelo número de símbolos alfabéticos que a compõem, mas sim pela análise à redundância na língua, considerando que o inverso da entropia é a redundância, ou seja, a organização do sistema em questão. Uma língua entrópica dispõe de um vocabulário rico, com palavras diferenciadas, que mostram o poder das combinatórias; uma língua pouco entrópica é pobre e repetitiva.
Em relação a imprevisibilidade, quanto maior for, será menor a chance de apreensão por parte do receptor, pois o receptor depende da ordem em que as mensagens são transmitidas. A imprevisibilidade total é correspondente à informação nula, ou seja, não há informação.
A medida da informação (ou surpresa) de um evento é uma função que decresce a medida em que a probabilidade do evento se eleva. Ela pode ser calculada a partir da fórmula de Hartley (1928):
Aqui, é a unidade da informação (Por exemplo: Informação binária, ). Já entropia pode ser explicitamente escrita como
onde é a probabilidade do i-ésimo resultado para a variável .
Uma maneira mais simples de medir a entropia é perceber que há duas possibilidades de ocorrência de um evento, como no caso do lançamento de uma moeda em um jogo de cara-ou-coroa com moeda viciada. Nesse caso temos p e q, onde q = 1-p, e a entropia do sistema é calculada como
Uma estatística quantica, no contexto da mecânica quântica e no da mecânica estatística, é a descrição de como a energia de cada um dos entes unitários constituintes de um ensemble está distribuida, dada uma energia total E constante, sob a restrição de que:
- a energia passa a ser quantizada;
- as partículas objeto de estudo passam a ser indistinguíveis.
Isso é feito expressando-se as probabilidades relativas de uma partícula com energia
De modo clássico, a probabilidade é dada por:
onde
é a chamada função de partição
Nos casos quanticos, o que muda é a questão da quantização do espaço de fase, o que impõe um "volume" mínimo de célula possível nesse espaço.
A Teoria da Informação teve inicialmente como destaque as questões técnicas, sendo uma das primeiras teorias a separar com nitidez a informação da significação. A Teoria da Informação está situada dentro da cibernética, onde a informação se mostra como uma medida probabilística. Esta teoria tem um grande interesse pelo funcionamento dos sinais, pelas transformações energéticas mediante a codificação da mensagem e sua de codificação. Ela opera com os seguintes conceitos:
- ruído;
- redundância;
- entropia;
- imprevisibilidade.
Em fontes contínuas, a codificação da informação gera ruído na mensagem, isso se dá pelo fato de que a fonte contínua precisaria de um vasto repertório de símbolos e que, como consequência, necessitaria uma capacidade de transmissão grande e, como é sabido, não existe um canal livre de ruído.
Shannon abordou, também o conceito de redundância é relacionado à entropia no sentido de que a redundância é tudo o que não é fundamental para ser entendido em uma determinada mensagem, ou seja, é entendida como algo complementar. Então é a medida de entropia para que a mensagem atinja a entropia máxima.
A entropia desejada de uma informação é a máxima que é dada pelas probabilidades equivalentes de ocorrer todos os símbolos.
A teoria da informação não estuda uma língua pelo número de símbolos alfabéticos que a compõem, mas sim pela análise à redundância na língua, considerando que o inverso da entropia é a redundância, ou seja, a organização do sistema em questão. Uma língua entrópica dispõe de um vocabulário rico, com palavras diferenciadas, que mostram o poder das combinatórias; uma língua pouco entrópica é pobre e repetitiva.
Em relação a imprevisibilidade, quanto maior for, será menor a chance de apreensão por parte do receptor, pois o receptor depende da ordem em que as mensagens são transmitidas. A imprevisibilidade total é correspondente à informação nula, ou seja, não há informação.
A medida da informação (ou surpresa) de um evento é uma função que decresce a medida em que a probabilidade do evento se eleva. Ela pode ser calculada a partir da fórmula de Hartley (1928):
Aqui, é a unidade da informação (Por exemplo: Informação binária, ). Já entropia pode ser explicitamente escrita como
onde é a probabilidade do i-ésimo resultado para a variável .
Uma maneira mais simples de medir a entropia é perceber que há duas possibilidades de ocorrência de um evento, como no caso do lançamento de uma moeda em um jogo de cara-ou-coroa com moeda viciada. Nesse caso temos p e q, onde q = 1-p, e a entropia do sistema é calculada como
Uma estatística quantica, no contexto da mecânica quântica e no da mecânica estatística, é a descrição de como a energia de cada um dos entes unitários constituintes de um ensemble está distribuida, dada uma energia total E constante, sob a restrição de que:
- a energia passa a ser quantizada;
- as partículas objeto de estudo passam a ser indistinguíveis.
Isso é feito expressando-se as probabilidades relativas de uma partícula com energia
De modo clássico, a probabilidade é dada por:
onde
é a chamada função de partição
Nos casos quanticos, o que muda é a questão da quantização do espaço de fase, o que impõe um "volume" mínimo de célula possível nesse espaço.
 [EQUAÇÃO DE DIRAC].
[EQUAÇÃO DE DIRAC].
 + FUNÇÃO DE RADIOATIVIDADE
+ FUNÇÃO DE RADIOATIVIDADE
 + FUNÇÃO DE TUNELAMENTO QUÂNTICO.
+ FUNÇÃO DE TUNELAMENTO QUÂNTICO. + ENTROPIA REVERSÍVEL
+ ENTROPIA REVERSÍVEL ![\sigma =q(n\mu _{n}+p\mu _{p})[\Omega .cm]^{{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53d1173dd9d9ec55715f1f4beb1ea5dcd4932bc8) FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA
FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA ENERGIA DE PLANCK
ENERGIA DE PLANCK

 [ESTADO QUÂNTICO]
[ESTADO QUÂNTICO]



































Comentários
Postar um comentário